En análisis de circuitos eléctricos, el análisis de nodos, o método de tensiones nodales es un método para determinar la tensión (diferencia de potencial) de uno o más nodos.
Cuando se analiza un circuito por las leyes de Kirchhoff, se podrían usar análisis de nodos (tensiones nodales) por la ley de corrientes de Kirchhoff (LCK) o análisis de malla (corrientes de malla) usando la ley de tensiones de Kirchhoff (LVK). En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero en cualquier instante, por lo que una carga  nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
 nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente usando álgebra lineal en un computador. Por el hecho de que forme ecuaciones muy sencillas, este método es una base para muchos programas de simulación de circuitos (por ejemplo, SPICE). Cuando los elementos del circuito no tienen conductancia, se puede usar una extensión más general del análisis de nodos: el análisis de nodos modificado.
Los ejemplos simples de análisis de nodos se enfocan en elementos lineales. Las redes no lineales (que son más complejas) también se pueden resolver por el análisis de nodos al usar el método de Newton para convertir el problema no lineal en una secuencia de problemas lineales.
EJEMPLOS


Se resuelve con respecto a V1:

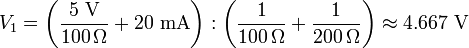
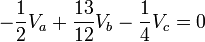



EJEMPLOS
Ejemplo 1: Caso básico
La única tensión desconocida en este circuito es V1. Hay tres conexiones en este nodo y por esta razón, 3 corrientes a considerar. Ahora se analiza todas las corrientes que pasan por el nodo, así:

Con ley de corrientes de Kirchhoff (LCK), tenemos:

Se resuelve con respecto a V1:

Finalmente, la tensión desconocida se resuelve sustituyendo valores numéricos para cada variable. Después de haber obtenido estas ecuaciones y conocer cada tensión, es fácil calcular cualquier corriente desconocida.
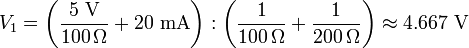
Ejemplo 2[editar]
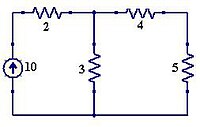
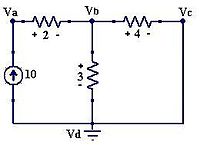
Ejemplo: Del circuito de la figura 4 debemos hallar los voltajes en sus diferentes nodos'
Solución:
- Se localizan todos los nodos del circuito.
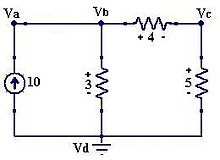
- Se busca el nodo con más conexiones y se le llama nodo de referencia Vd (Figura 5).
- No hay fuentes de tensión.
- Se le asignan variables a los nodos Va, Vb y Vc
- Se plantean las ecuaciones según las leyes de Kirchhoff, así:
- Para calcular el voltaje en el nodo Va, decimos que la resistencia de
 tiene la polaridad de la Figura 5. Así
tiene la polaridad de la Figura 5. Así
- Para calcular el voltaje en el nodo Va, decimos que la resistencia de
-

- simplificando:
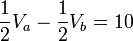
- Para calcular el voltaje en el segundo nodo (Vb) las resistencias que van a dicho nodo tendrán la polaridad de la Figura 6:
- factorizando obtenemos
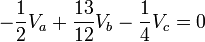
- Para la polaridad del nodo Vc asumimos así:

-
- factorizando obtenemos:

Sistema de ecuaciones: Obtenemos un sistema de ecuaciones del cual podemos determinar los valores del los voltajes en los nodos.

Solucionando el sistema lineal, nos da como resultado los voltajes: 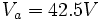 ,
,  y
y 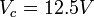
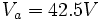 ,
,  y
y 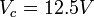


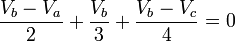
No hay comentarios:
Publicar un comentario