Para aplicar las leyes de Kirchhoff a un circuito eléctrico, se deben definir primero las distintas partes en
las que se puede dividir un circuito, estas son:
o NODO: Es un punto del circuito donde se unen tres o más conductores.
o RAMA: Es la parte del circuito situada entre dos nodos.
o MALLA: Es la parte del circuito que puede ser recorrida sin pasar dos veces por el mismo
sitio.
La ley de corriente de Kirchhoff como esta escrita es aplicable solamente a circuitos de corriente continua (i.e., sin corriente alterna, sin transmisión de señal). Puede ser extendida para incluir flujos de corriente que dependen del tiempo, pero esto está más allá del enfoque de esta sección.
Cada nodo se usa para formar una ecuación que son resueltas simultáneamente, y la solución de ecuaciones simultáneas entregan el voltaje en cada nodo.
En resumen: en un nodo la corriente que entra es la misma que sale de él.

LEY DE OHM
La ley de Ohm se aplica a cualquier parte del circuito tanto como al circuito completo. Puesto que la corriente es la misma en las tres resistencias de la figura 1, la tensión total se divide entre ellas.
La tensión que aparece a través de cada resistencia (la caída de tensión) puede obtenerse de la ley de Ohm.
Ejemplo: Si la tensión a través de Rl la llamamos El, a través de R2, E2, y a través de R3, E3, entonces
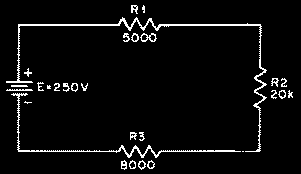
figura1
El = IxRI = 0,00758 X 5000 = 37,9 V
E2 = IxR2 = 0,00758 X 20.000 = 151,5 V
E3 = IxR3 = 0,00758 X 8000 = 60,6 V
En un nodo se cumple que, la suma algebraica de las corrientes en el mismo, es igual a cero.
Para realizar la suma algebraica de las intensidades, se tendrá que tener en cuanta el signo de estas
intensidades. Se tomará como convenio que, el signo de las intensidades será el siguiente:
o Positivo, cuando el sentido de la corriente es de entrada al nodo.
o Negativo, cuando el sentido sea de salida del nodo.
En el nodo de la figura anterior, el resultado de aplicar la primera ley de Kirchhoff, sería el siguiente:
I1+I2-I3-I4 = 0
NOTA: En una rama, puesto que todos los elementos que la forman están conectados en serie, el
valor y sentido de la corriente eléctrica en todos los puntos y elementos de la misma, serán iguales.
La primera ley de Kirchhoff describe con precisión la situación del circuito: La suma de las tensiones en un bucle de corriente cerrado es cero. Las resistencias son sumideros de potencia, mientras que la batería es una fuente de potencia, por lo que la convención de signos descrita anteriormente hace que las caídas de potencial a través de las resistencias sean de signo opuesto a la tensión de la batería. La suma de todas las tensiones da cero. En el caso sencillo de una única fuente de tensión, una sencilla operación algebraica indica que la suma de las caídas de tensión individuales debe ser igual a la tensión aplicada.
E= El + E2 + E3
E= 37,9 + 151,5 + 60,6
E= 250 V
En problemas como éste, cuando la corriente es suficientemente pequeña para ser expresada en miliamperios, se puede ahorrar cantidad de tiempo y problemas expresando la resistencia en kilohms mejor que en ohms. Cuando se sustituye directamente la resistencia en kilohms en la ley de Ohm, la corriente será en miliamperios si la FEM está en voltios.
Resistencias en paralelo
En un circuito con resistencias en paralelo, la resistencia total es menor que la menor de las resistencias presentes. Esto se debe a que la corriente total es siempre mayor que la corriente en cualquier resistencia individual. La fórmula para obtener la resistencia total de resistencias en paralelo es
R=1 / (1/R1)+(1/R2)+(1/R3)+...
donde los puntos suspensivos indican que cualquier número de resistencias pueden ser combinadas por el mismo método.
En el caso de dos resistencias en paralelo (un caso muy común), la fórmula se convierte en
R= R1xR2 / R1+R2
Ejemplo: Si una resistencia de 500 O está en paralelo con una de 1200 O, la resistencia total es:
R = 500x1200/500+1200=600000 / 1700 =353
SEGUNDA LEY DE KIRCHHOFF (LEY DE TENSIONES):
En una malla se cumple que, la suma algebraica de las fuerzas electromotrices (f.e.m.s), es igual a la suma de las caídas de tensión en la misma.
Hay otra solución para el problema. Suponga que las tres resistencias del ejemplo anterior se conectan en paralelo como se muestra en la figura 2.
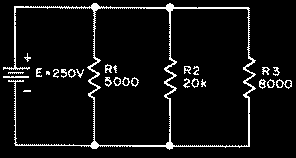
figura2
La misma FEM, 250 V, se aplica a todas las resistencias.
La corriente en cada una puede obtenerse de la ley de Ohm como se muestra más abajo, siendo I1 la corriente a través de Rl, I2 la corriente a través de R2, e I3 la corriente a través de R3.
Por conveniencia, la resistencia se expresará en kilohms, por tanto la corriente estará en miliamperios.
I1=E / R1=250 / 5 = 50mA
I2 = E / R2 = 250 / 20 =12,5mA
I3 = E / R3 = 250 / 8 = 31,25 mA
La corriente total es
I total =I1 + 12 + 13 = 50 + 12,5 + 31,25 = 93,75 mA
Este ejemplo ilustra la ley de corriente de Kirchhoff.
"La corriente que circula hacia un nodo o punto de derivación es igual a la suma de las corrientes que abandonan el nodo o derivación."
Por tanto, la resistencia total del circuito es
Rtotal= E / I = 250 / 93,75 = 2,667 KO
EJEMPLOS:
Ejemplo 1


Ejemplo 2
Hallar IA, ID, IF

No hay comentarios:
Publicar un comentario